 Machines that deal with numbers and perform useful calculations have a long history, gradually increasing in power and flexibility over the course of several centuries. Machines which deal intelligently with words, and produce sensible prose, however, seem like a relatively recent aspiration. There were simple humanoid automata in Descartes’ day, and impressively sophisticated ones during the eighteenth century: such ‘robots’ naturally gave rise to the speculation that they might one day speak as well as mimic human beings in other ways. But surely Turing was the first person to propose in earnest a machine which could produce worthwhile words of its own?
Machines that deal with numbers and perform useful calculations have a long history, gradually increasing in power and flexibility over the course of several centuries. Machines which deal intelligently with words, and produce sensible prose, however, seem like a relatively recent aspiration. There were simple humanoid automata in Descartes’ day, and impressively sophisticated ones during the eighteenth century: such ‘robots’ naturally gave rise to the speculation that they might one day speak as well as mimic human beings in other ways. But surely Turing was the first person to propose in earnest a machine which could produce worthwhile words of its own?
There were, of course, many more or less mechanical ancient systems designed to produce oracles or mystical insights. The I Ching is one interesting example: the basic apparatus is a collection of texts, with the appropriate one for a given occasion to be looked up using randomly-generated patterns. (the patterns are produced by throwing sticks, though coins and other methods can be used). If that was all there was to it, it would seem to be more or less computational in nature, albeit very simple – not very different, in some ways, to the sortes Virgilianae, the Roman system in which a random text from Virgil was taken as oracular. Leibniz took the symbols which identify the I Ching texts, which consist of sets of broken and unbroken lines, to be a binary numbering system, which would strengthen the resemblance to a modern program. In fact, although the symbols do lend themselves to a binary interpretation, that isn’t the way they were designed or understood by the original practitioners. More fundamental, the significance of the results properly requires meditation and interpretation; it isn’t really a purely mechanical business.
It is just conceivable (I think) that Roger Bacon considered the possibility of a talking machine. There is an absurd story of how he and another friar constructed a brass head which would have pronounced words of oracular wisdom had not their servant botched the experiment by ignoring the vital moment when the head first spoke. This tale was perhaps influenced by earlier stories about mechanical talking heads, such as the bull’s head Pope Silvius (an innovative mathematician, interestingly enough) was said to have had, which would return infallible yes or no answers to any question. There is no evidence that Bacon ever contemplated a talking machine, but a procedure for generating intelligible sentences would have been the sort of thing which might have interested him, and I like to think that the brass head story is a distorted echo of some long-lost project along these lines.
In any case, there is one incontrovertible example from about the same time; Ramon Llull’s Ars Magna provides a mechanical process for generating true statements and even proofs. Llull, born around 1232, enjoyed a tremendous reputation in his day, and was famous enough to have had his name anglicised as ‘Raymond Lully’. He was better acquainted with Jewish and Arabic learning than most medieval scholars, and may possibly have been influenced by the Kabbalistic tradition of generating new insights through new permutations of the words and letters of holy texts. He wrote in both Arabic and the vernacular, and among other achievements is regarded as a founding father of Catalan literature.
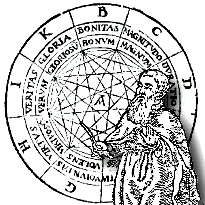
The Ars Magna has a relatively complex apparatus and uses single words rather than extended texts as its basic unit. The core of the whole thing is the table below.
| Absolute principles |
Relative principles |
Questions | Subjects | Virtues | Vices | |
| B | Goodness | Difference | Whether | God | Justice | Avarice |
| C | Greatness | Concord | What | Angel | Prudence | Gluttony |
| D | Eternity | Opposition | Whence | Heaven | Fortitude | Luxury |
| E | Power | Priority | Which | Man | Temperance | Pride |
| F | Wisdom | Centrality | How many | Imaginative | Faith | Sloth |
| G | Will | Finality | What kind | Sensitive | Hope | Envy |
| H | virtue | Majority | When | Vegetative | Charity | Anger |
| I | Truth | Equality | Where | Elemental | Patience | Untruthfulness |
| K | Glory | Minority | How – with what | Instrumental | Piety | Inconstancy |
Llull provides four figures in the form of circular or tabular diagrams which recombine the elements of this table in different ways. Very briefly, and according to my shaky understanding, the first figure produces combinations of absolute principles – ‘Wisdom is Power’, say. The second figure applies the relative principles – ‘Angels are different from elements’. The third brings in the questions – ‘Where is virtue final?’. The fourth figure is perhaps the most exciting: it take the form of a circular table which is included in the book as a paper wheel which can be rotated to read off results. This extraordinary innovation has led to Llull acquiring yet another group of fans – this is regarded as the forerunner of pop-up books. The fourth figure combines the contents of four different table cells at once to generate complex propositions and questions.
The kind of thinking going on here is not, it seems to me, all that different from what goes into the creation of simple sentence-generating programs today, and it represents a remarkable intellectual feat. But the weaknesses of the system are obvious. First, the apparatus is capable of generating propositions which are false or heretical, or (perhaps more worrying to us) highly opaque, open to various different interpretations. Llull implicitly recognises this: in fact, to perform some of the tasks he proposes – such as the construction of syllogisms – a good deal of interpretation and reasoning outside the system is required: the four figures alone merely give you a start. Second, the Ars Magna is quite narrowly limited in scope – it really only deals with a restricted range of theological and metaphysical issues. Of course, this reflects Llull’s preoccupations, but he also remained unworried by it because of two beliefs which then seemed natural but now are virtually untenable. One is that the truths of Christianity are ultimately as provable as the truths of geometry. The other is that the world is fully categorisable.
Llull’s system, and many others since, is ultimately combinatorial. It simply puts together combinations of elements. In order to deal with the world at large successfully, such a system has to have a set of elements which in some sense exhaust the universe – which cover everything there is or could be. When we put it like that, it seems obvious that there is no way of categorising or analysing the world into a finite set of elements, but the belief is a tenacious one. Even now, some are tempted to believe that with a big enough encyclopaedia, a computer will be able to deal with raw reality. But any such project sends the finite out to do battle with the infinite. Perhaps it would help to realise just how old – how medieval – this particular project really is.
